Answer : The enthalpy of mixture for this solution is, 5.4 kJ/mol
Explanation :
As we are given that 20 wt% of A solution. That means,
In 100 g of solution, there 20 g of A and 80 g of B.
Now we have to calculate the moles of A and B.
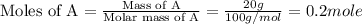

Now we have to calculate the total number of moles of solution.
Total number of moles of solution = Moles of A + Moles of B
Total number of moles of solution = 0.2 + 1.6
Total number of moles of solution = 1.8 mole
Now we have to calculate the amount of energy removed.
As, 1 mole of solution released energy = 1 kJ
So, 1.8 moles of solution released energy = 1.8 × 1 kJ = 1.8 kJ
Now we have to calculate the enthalpy of mixing of A and B.
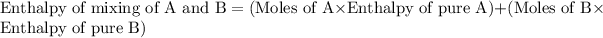
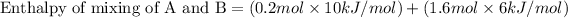
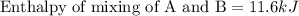
Now we have to calculate the actual enthalpy of mixing of solution.
Actual enthalpy of mixing of solution = 11.6 - 1.8 = 9.8 kJ
Now we have to calculate the enthalpy of mixture in kJ/mol.
Enthalpy of mixture =
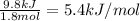
Therefore, the enthalpy of mixture for this solution is, 5.4 kJ/mol