Step-by-step explanation:
As it is given that mixture (contains 9 mol % A and 91% B) and it is flowing at a rate of 800 kg/h.
Hence, calculate the molecular weight of the mixture as follows.
Weight =
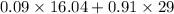
= 27.8336 g/mol
And, molar flow rate of air and mixture is calculated as follows.
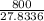
= 28.74 kmol/hr
Now, applying component balance as follows.

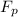 = 43.11 kmol/hr
= 43.11 kmol/hr

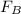 = 43.11 - 28.74
= 43.11 - 28.74
= 14.37 kmol/hr
So, mass flow rate of pure (B), is
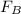 =
=

= 416.73 kg/hr
According to the product stream, 6 mol% A and 94 mol% B is there.
Molecular weight of product stream =
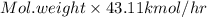
=
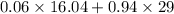
= 28.22 g/mol
Mass of product stream = 1216.67 kg/hr
Hence, mole of
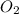 into the product stream is as follows.
into the product stream is as follows.
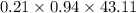
=

= 272.31 kg/hr
Therefore, calculate the mass % of
 into the stream as follows.
into the stream as follows.
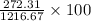
= 22.38%
Thus, we can conclude that the required flow rate of B is 272.31 kg/hr and the percent by mass of
 in the product gas is 22.38%.
in the product gas is 22.38%.