Question

The force of attraction between a divalent cation and a divalent anion is 1.12 x 10-8 N. If the ionic radius of the cation is 0.071 nm, what is the anion radius?

Answer 1

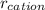`r_(cation)` = 0.2162 nm

Step-by-step explanation:

The force of attraction can be written as:

`F=\frac Z_(anion){r^2}`

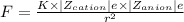
Where,

K is the Coulomb's constant having value 9×10⁹ N. m²/C²

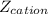`Z_(cation)` is the charge on the cation

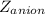`Z_(anion)` is the charge on the anion

e is electronic charge =
`1.602* 10^(-19)\ C`

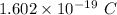
r is the distance between the cation and anion and in bond, it is the sum of the ionic radius of cation and anion

So,

Given, F =
`1.12* 10^(-8)\ N`

`Z_(cation)=Z_(anion)=2`

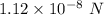
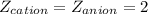
Applying in the equation,

`1.12* 10^(-8)=(9* 10^9* 2* 1.602* 10^(-19)* 2* 1.602* 10^(-19))/(r^2)`

`r^2=(9* \:10^9* \:2* \:1.602* \:10^(-19)* \:2* \:1.602* \:10^(-19))/(1.12* \:10^(-8))`

`r^2=(10^(-29)\cdot \:92.390544)/(10^(-8)\cdot \:1.12)`

`r=0.2872* 10^(-9)\ m`

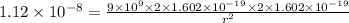
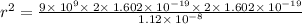
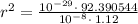
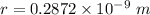
Also, 1 m =
`10^(-9)\ nm`

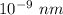
So, r = 0.2872 nm

Also,

`r=r_(cation)+r_(anion)`

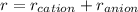
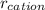`r_(cation)` = 0.071 nm

Thus,

`0.2872\ nm=0.071\ nm+r_(anion)`

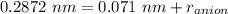
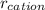`r_(cation)` = 0.2162 nm