Answer and explanation:
Given : A driving exam consists of 29 multiple-choice questions. Each of the 29 answers is either right or wrong. Suppose the probability that a student makes fewer than 6 mistakes on the exam is 0.26 and that the probability that a student makes from 6 to 20 (inclusive) mistakes is 0.53.
Let X be the number of mistake


To find : The probability of each of the following outcomes.
a) A student makes more than 20 mistakes
i.e.
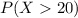
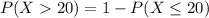

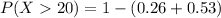


b. A student makes 6 or more mistakes
i.e.
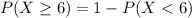
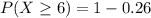

c. A student makes at most 20 mistakes
i.e.
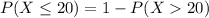
Using 'a' part

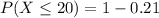

d. Which two of these three events are complementary?
The complement of an event happening is the exact opposite: the probability of it not happening.
According to definition,
Option a and c are complementary events.