Question

The distribution of passenger vehicle speeds traveling on a certain freeway in California is nearly normal with a mean of 73.7 miles/hour and a standard deviation of 4.77 miles/hour. (a) What percent of passenger vehicles travel slower than 80 miles/hour? (Round your answer to two decimal places.) % (b) What percent of passenger vehicles travel between 60 and 80 miles/hour? (Round your answer to two decimal places.) % (c) How fast do the fastest 5% of passenger vehicles travel? (Round your answer to four decimal places.) mph (d) The speed limit on this stretch of the freeway is 70 miles/hour. Approximate what percentage of the passenger vehicles travel above the speed limit on this stretch of the freeway. (Round your answer to two decimal places.)

Answer 1

A) 90.32%

B) 90.11%

C) 81.546 miles per hour

D)77.93%

Explanation:

Given data:

speed = 73.7 miles/hour

standard deviation = 4.77 miles /hour

a)
`P(X< 80) = P(z< (80 - 73.7)/(4.77)`

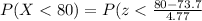
= P (z< 1.31)

= 0.90320 = 90.32%

b)
`P(60 < X< 80) = P((60 - 73.7)/(4.77) < z< (80 - 73.7)/(4.77))`

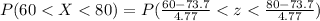
= P (-2.872< z< 1.31)

= P (z<1.31) - P(z<-2.87)

= 0.90320 - 0.00205

= 0.90115 = 90.11%

c) P(X <X) = 0.95

z = 1.645

`(x - 73.7)/(4.77) = 1.645`

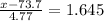
x = 81.546 miles per hour

`d)P(X< 70) = P(z> (70 - 73.7)/(4.77))`

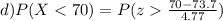
= P (z> -0.775)

= 0. 0.7793 = 77.93%