Answer:
a photon with a wavelength of 2625 nm is released
Step-by-step explanation:
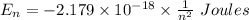
For transitions:
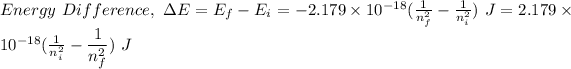
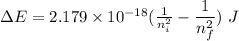
Also,
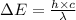
Where,
h is Plank's constant having value

c is the speed of light having value
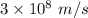
So,


So,

Given,

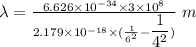


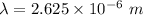
1 m = 10⁻⁹ nm
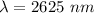
From coming from higher energy level to lower, energy is released.
Hence, correct option is - a photon with a wavelength of 2625 nm is released