Question

In a certain liberal arts college with about 10,000 students, 53% are males. If two students from this college are selected at random, what is the probability that they are of the same gender? 0.2491 Your answer should be rounded to 4 decimal places. Feedback Incorrect. Hint: P(same gender)=P(MM or FF) = P(MM) + P(FF) Note: the events of MM and FF are mutually exclusive, i.e., they cannot happen at the same time. The correct probability is: 0.5018

Answer 1

There is a 50.18% probability that they are of the same gender.

Explanation:

We have these following percentages:

53% of the students are males.

47% of the students are females.

If two students from this college are selected at random, what is the probability that they are of the same gender?

The probability that each is male is 53%. So the probability of both being males is

`P_(MM) = 0.53*0.53 = 0.2809`

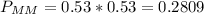
The probability that each is female is 47%. So the probability of both being females is

`P_(FF) = 0.47*0.47 = 0.2209`

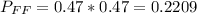
The probabilty that both are the same gender is:

`P = P_(MM) + P_(FF) = 0.2809 + 0.2209 = 0.5018`

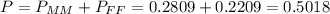
There is a 50.18% probability that they are of the same gender.