Answer:
The no. of variations in sign is 3
Explanation:
Variation in sign occurs when every single time a negative product is produced by a pair of consecutive terms.
Therefore, the determination of the number of changes in sign in the given sequence is must.
Therefore, we take the product of the pair of consecutive terms as:
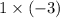 = - 3, variation in sign
= - 3, variation in sign
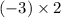 = - 6, variation in sign
= - 6, variation in sign
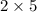 = 10, no sign variation
= 10, no sign variation
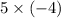 = - 20, variation in sign
= - 20, variation in sign
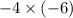 = 24, no sign variation
= 24, no sign variation