Question

What is the wavelength in picometers for an electron moving at 1,495 km ?

Answer 1

Wavelength = 486.51 pm

Step-by-step explanation:

The expression for the deBroglie wavelength is:

`\lambda=\frac {h}{m* v}`

Where,

`\lambda` is the deBroglie wavelength

h is Plank's constant having value
`6.626* 10^(-34)\ Js`

m is the mass of electron having value
`9.11* 10^(-31)\ kg`

v is the speed of electron.

Given that v = 1495 km/s (Corrected from source)

Also, 1 km = 1000 m

So, v = 1495000 m/s

Applying in the equation as:

`\lambda=\frac {h}{m* v}`

`\lambda=(6.626* 10^(-34))/(9.11* 10^(-31)* 1495000)\ m`

`\lambda=(10^(-34)* \:6.626)/(10^(-31)* \:13619450)\ m`

`\lambda=(6.626)/(13619450000)\ m`

`\lambda=4.8651* 10^(-10)\ m`

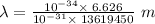
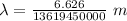
Also, 1 m = 10¹² pm

So, Wavelength = 486.51 pm