Question

The number of bacteria in a refrigerated food product is given by N ( T ) = 27 T 2 − 180 T + 100 N(T)=27T2-180T+100, 7 < T < 37 7

Answer 1

`N(T(t))=432t^2-374.4t-118.88`

The number of Bactria after 5.8 hours is 12242.

Explanation:

The number of bacteria in a refrigerated food product is given by

`N(T)=27T^2-180T+100`

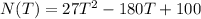
where, T is the temperature of the food.

When the food is removed from the refrigerator, then the temperature is given by

`T(t)=4t+1.6`

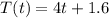
We need to find the composite function N(T(t)).

`N(T(t))=N(4t+1.6)`

`N(T(t))=27(4t+1.6)^2-180(4t+1.6)+100`

`N(T(t))=432t^2+345.6t+69.12-720t-288+100`

`N(T(t))=432t^2-374.4t-118.88`

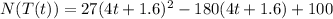
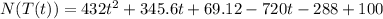
where N(T(t)) is the number of bacteria after t hours.

Substitute t=5.8 in the above function.

`N(T(5.8))=432(5.8)^2-374.4(5.8)-118.88`

`N(T(5.8))=14532.48-2290.4`

`N(T(5.8))=12242.08`

`N(T(5.8))\approx 12242`

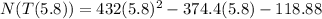
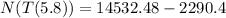
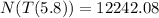
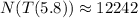
Therefore, the number of Bactria after 5.8 hours is 12242.