Answer:
According to the passage, we have the next equation:
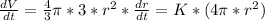
where "K" is a proportional constant
Leaving at the end with the next equation:
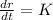
Integrating the equation, we have:

where "C" is a constant
Then, we have the 2 conditions for the problem:
1) t=0 → r=10
Replacing in the equation, we have C = 10
2) t=5 → r=8
Replacing in the equation, we have K = -0.4
Finally, the time which the snowball will be completely melted will be when r = 0. So replacing in the equation

t = 25 minutes