Question

Tony consumes an energy drink that contains caffeine. After consuming the energy drink, the amount of caffeine in Tony's body decreases exponentially. The 10-hour decay factor for the number of mg of caffeine in Tony's body is 0.2722. What is the 5-hour growth/decay factor for the number of mg of caffeine in Tony's body? What is the 1-hour growth/decay factor for the number of mg of caffeine in Tony's body? If there were 176 mg of caffeine in Tony's body 1.23 hours after consuming the energy drink, how many mg of caffeine is in Tony's body 2.23 hours after consuming the energy drink? mg

Answer 1

10-hour decay factor = 0.13012

5-hour decay factor = 0.52173

1-hour decay factor = 0.87799

154.52624 mg of caffeine

Explanation:

Exponential decay is the decrease in a quantity N according to:

`N(t) = N_(0) e^(-kt)`

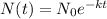
where

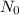`N_(0)` = initial value of quantity N

N(t) = quantity N at time t

k = decay constant associated to physical properties of N

`e^(-kt)` = decay factor

Substituting the values from the problem:

t = 10 hours

`e^(-kt)` = 0.2722

Then, solving for k:

`0.2722 =e^(-k*10)\\ ln(0.2722)=ln(e^(-k*10))\\ln(0.2722)=-k*10\\(-ln(0.2722))/(10) =k\\0.13012=k`

With the value of the decay constant k, you could calculate the decay factor at any given time. For t = 5 hours, the decay factor is given by:

`e^(-kt)=e^(-0.13012*5)  \\e^(-kt)=0.52173`

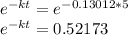
For t = 1 hour, the decay factor is given by:

`e^(-kt)=e^(-0.13012*1)  \\e^(-kt)=0.87799`

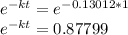
If there are 176 mg in Tony's body 1.23 hours after consuming the energy drink, then you could take this value as the initial value of quantity N, i.e.
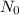`N_(0)`. Then, the quantity of caffeine in Tony's body 2.23 hours later is just the quantity N(t) one hour later from the initial value (1.76 mg), then:

`N(t) = N_(0)e^(-kt)\\ N(1) = (176mg)e^(-k*1)\\N(1)=(176mg)(0.87799)\\N(1)=154.52624 mg`

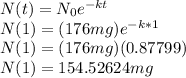
Note that
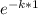`e^(-k*1)` is the 1-hour decay factor previously calculated.