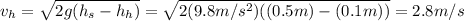Question

Consider a cylinder with water filled to a height of 50 cm. At a height of 10 cm is a hole in the side of the cylinder . Assuming that there is no viscous drag of the fluid flowing through the hole, what is the velocity of the fluid squirting out of it? (Hint: you will need to use Bernoulli, and make the assumption that the pressure of the water just as it leaves the hole, since it is in contact with the air, is just atmospheric pressure.)

Answer 1

`v_h=2.8m/s`

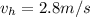
Step-by-step explanation:

The Bernoulli equation tells us that in a fluid
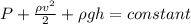`P+(\rho v^2)/(2)+\rho gh=constant`, so we will apply this to a point on the surface and a point on the hole.

For a point on the surface (at height
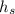`h_s`) the velocity will be approximated to 0m/s since we assume it barely moves (unless other information is given), so we have:

`P_(atm)+\rho gh_s=constant`

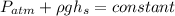
For a point on the hole (at height
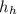`h_h` and velocity of the fluid
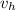`v_h`) we have:

`P_(atm)+(\rho v_h^2)/(2)+\rho gh_h=constant`

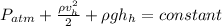
Since both constant are the same, cancelling
`P_(atm)` we have:

`\rho gh_s=(\rho v_h^2)/(2)+\rho gh_h`

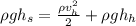
Which means:

`(\rho v_h^2)/(2)=\rho gh_s-\rho gh_h=\rho g(h_s-h_h)`

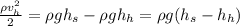
So the velocity of the fluid flowing through the hole will be:

`v_h=√(2g(h_s-h_h))=√(2(9.8m/s^2)((0.5m)-(0.1m)))=2.8m/s`