Answer:
The probability that a repair time exceeds 8 hours is
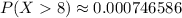
The conditional probability that a repair takes at least 13 hours, given that it takes more than 9 hours is

Explanation:
A continuous random variable X is said to have an exponential distribution with parameter
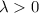 shown as
shown as
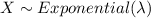 , if its probability density function is given by
, if its probability density function is given by
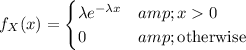
Let X denote the time require to repair a machine.
(a) The probability that a repair time exceeds 8 hours;
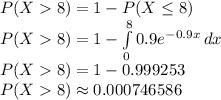
(b) The conditional probability that a repair takes at least 13 hours, given that it takes more than 9 hours;
We want to find
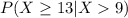 .
.
