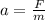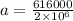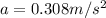Answer:
Step-by-step explanation:
As we know that the force due to propeller when it will push the water backwards is given as

now we know that
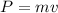
so we have
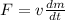
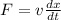
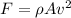
here we know that
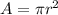
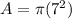

now the force is given as
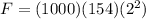
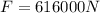
now the acceleration of the ship is given by Newton's II law