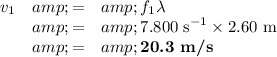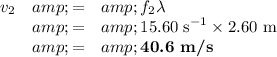Answer:
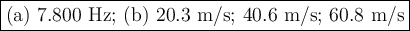
Step-by-step explanation:
a) Fundamental frequency
A harmonic is an integral multiple of the fundamental frequency.
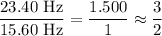
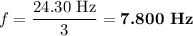
b) Wave speed
(i) Calculate the wavelength
In a fundamental vibration, the length of the string is half the wavelength.
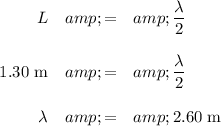
(b) Calculate the speed s