Question

A person gets 13 cards of a deck. Let us call for simplicity the types of cards by 1,2,3,4. In How many ways can we choose 13 cards, so that so that there are 5 of type 1, there are 4 of type 2, there are 2 of type 3 and there are 2 of type 4?

Answer 1

There are 5,598,527,220 ways to choose 5 cards of type 1, 4 cards of type 2, 2 cards of type 3 and 2 cards of type 4 from a set of 13 cards.

Step-by-step explanation:

The crucial point of this problem is to understand the possible ways of choosing any type of card from the 13-card deck.

This is a problem of combination since the order of choosing them does not matter here, that is, the important fact is the number of cards of type 1, 2, 3 or 4 we can get, no matter the order that they appear after choosing them.

So, the question for each type of card that we need to answer here is, how many ways are there of choosing 5 cards of type 1, 4 cards of type 2, 2 cards of type 3 and 2 are of type 4 from the deck of 13 cards?

The mathematical formula for combinations is
`\\ (n!)/((n-k)!k!)`, where n is the total of elements available and k is the size of a selection of k elements from which we can choose from the total n.

Then,

Choosing 5 cards of type 1 from a 13-card deck:

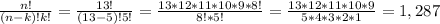`(n!)/((n-k)!k!) = (13!)/((13-5)!5!) = (13*12*11*10*9*8!)/(8!*5!) = (13*12*11*10*9)/(5*4*3*2*1) = 1,287`, since
`\\ (8!)/(8!) = 1`.

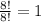Choosing 4 cards of type 2 from a 13-card deck:

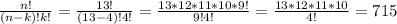`\\ (n!)/((n-k)!k!) = (13!)/((13-4)!4!) = (13*12*11*10*9!)/(9!4!) = (13*12*11*10)/(4!)= 715`, since
`\\ (9!)/(9!) = 1`.

Choosing 2 cards of type 3 from a 13-card deck:

`\\ (n!)/((n-k)!k!) =(13!)/((13-2)!2!) = (13*12*11!)/(11!2!) = (13*12)/(2!) = 78`, since
`\\ (11!)/(11!)=1`.

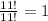Choosing 2 cards of type 4 from a 13-card deck:

It is the same answer of the previous result, since

`\\ (n!)/((n-k)!k!) = (13!)/((13-2)!2!) = 78`.

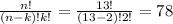We still need to make use of the Multiplication Principle to get the final result, that is, the ways of having 5 cards of type 1, 4 cards of type 2, 2 cards of type 3 and 2 cards of type 4 is the multiplication of each case already obtained.

So, the answer about how many ways can we choose 13 cards so that there are 5 of type 1, there are 4 of type 2, there are 2 of type 3 and there are 2 of type 4 is:

1287 * 715 * 78 * 78 = 5,598,527,220 ways of doing that (or almost 6 thousand million ways).

In other words, there are 1287 ways of choosing 5 cards of type 1 from a set of 13 cards, 715 ways of choosing 4 cards of type 2 from a set of 13 cards and 78 ways of choosing 2 cards of type 3 and 2 cards of type 4, respectively, but having all these events at once is the multiplication of all them.