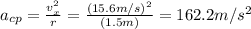Answer:
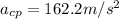
Step-by-step explanation:
The time the stone takes to fall can be calculated considering only the vertical component with the formula:
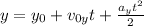
Taking the inital height as 0m and downward direction positive, since it departs from (vertical) rest we have:
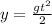
Which gives us a time:
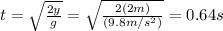
Horizontally, on that time the stone travelled a distance x=10m, which means its horizontal speed was:
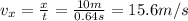
Since this speed is the tangential velocity while whirling, the centripetal acceleration of the stone was: