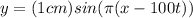Answer:
Part a)
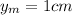
Part b)
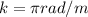
Part c)
v = 100 m/s
Part d)
since wave is moving in +x direction
so here the sign must be negative
so complete wave equation is
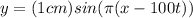
Step-by-step explanation:
As we know that the wave equation is given as
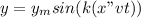
here we know that
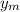 = maximum displacement of the particle
= maximum displacement of the particle
Part a)
maximum displacement = amplitude
so here we know that
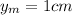
Part b)
k =
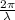
here we know that length of the string is 3 m
it consist of 3 loops
so we will have
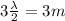

so we have
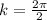
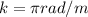
Part c)
v = wave speed
v = 100 m/s
Part d)
since wave is moving in +x direction
so here the sign must be negative
so complete wave equation is