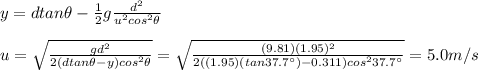Question

Salmon often jump waterfalls to reach their

breeding grounds.
Starting downstream, 1.95 m away from a
waterfall 0.311 m in height, at what minimum
speed must a salmon jumping at an angle of
37.7° leave the water to continue upstream?
The acceleration due to gravity is 9.81 m/s2.
Answer in units of m/s.

Answer 1

5.0 m/s

Step-by-step explanation:

The horizontal motion of the salmon is uniform, so the horizontal component of the salmon's velocity is constant and it is

`v_x = u cos \theta`

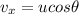
where u is the initial speed and
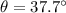`\theta=37.7^(\circ)`. The horizontal distance travelled by the salmon is

`d=v_x t = (ucos \theta)t`

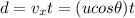
where d = 1.95 m and t is the time needed to reach the final point.

Re-arranging for t,

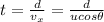`t=(d)/(v_x)=(d)/(u cos \theta)` (1)

Along the vertical direction, the equation of motion is

`y=h+u_y t -(1)/(2)gt^2`

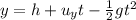
where:

y = 0.311 m is the final height reached by the salmon

h = 0 is the initial height

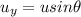`u_y = u sin \theta` is the vertical component of the initial velocity of the salmon

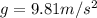`g=9.81 m/s^2` is the acceleration of gravity

t is the time

Substituting t as found in eq.(1), we get the equation

`y=(u sin \theta) (d)/(u cos \theta)- (1)/(2)g(d^2)/(u^2 cos^2 \theta)=d tan \theta - (1)/(2)g(d^2)/(u^2 cos^2 \theta)`

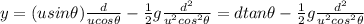
and we can solve this formula for u, the initial speed of the salmon:

`y=d tan \theta - (1)/(2)g(d^2)/(u^2 cos^2 \theta)\\\\u=\sqrt{(gd^2)/(2(dtan \theta -y)cos^2 \theta)}=\sqrt{((9.81)(1.95)^2)/(2((1.95)(tan 37.7^(\circ)) -0.311)cos^2 37.7^(\circ))}=5.0 m/s`