Answer:
The probability that a randomly selected boy in secondary school will
take longer than 335 seconds to run the mile is 0.9893 ⇒ answer B
Explanation:
- A physical fitness association is including the mile run in its
secondary-school fitness test
- The time for this event for boys in secondary school is known to
possess a normal distribution with a mean of 450 seconds and a
standard deviation of 50 seconds
∴ μ = 450 seconds
∴ σ = 50 seconds
- We need to find the probability that a randomly selected boy in
secondary school will take longer than 335 seconds to run the mile
- We must to find z-score for x > 335 seconds
∵ z = (x - μ)/σ
∵ x = 335 seconds , μ = 450 seconds , σ = 50 seconds
- substitute the values in the rule above
∴ z =
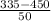 = -2.3
= -2.3
- Use the normal distribution table of z to find the corresponding area
of z-score
∵ P(-2.3) = 0.01072
- We need to find the area to the right of the z-score
∴ P( x > 335) = 1 - 0.01072 = 0.9893
* The probability that a randomly selected boy in secondary school
will take longer than 335 seconds to run the mile is 0.9893