Answer : The pressure inside the bottle is 49.2 atm
Explanation :
First we have to calculate the mass of helium.

Now we have to calculate the moles of helium.
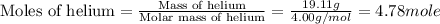
Now we have to calculate the moles of air in the container.
Using ideal gas equation :
PV = nRT
where,
P = Pressure of air = 1.0 atm
V = Volume of air = 2.50 L
n = number of moles of air = ?
R = Gas constant =
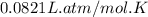
T = Temperature of air = 125 K
Putting values in above equation, we get:
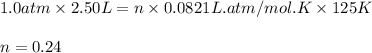
Now we have to calculate the pressure of individual components at
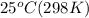 .
.
Pressure of helium:
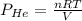
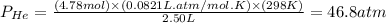
Pressure of air :
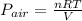
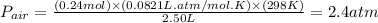
The overall pressure =
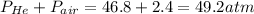
Therefore, the pressure inside the bottle is 49.2 atm