Question

A geostationary satellite is a satellite which always hangs above the same location on the Earth. That is, as the earth spins under the satellite once every 24 hours (actually 23 h 56 m 4.1 s, you can look through the Wikipedia article on "Siderial time" if you want to know why it is not exactly 24 h), the satellite completes exacly one orbit. Find the radius of a geostationary orbit. The mass of the Earth is 5.97 × 1024 kg. Explain your reasoning!

Answer 1

r=42227Km using 24h, r=42150Km using the exact given value.

Step-by-step explanation:

The force that acts on the satellite of mass m is the gravitational pull of the Earth, of mass M. If the distance between their centers is r, we know that this gravitational force must be:

`F_G=(GMm)/(r^2)`

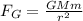
Where
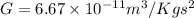`G=6.67*10^(-11)m^3/Kgs^2` is the gravitational constant.

The satellite moves in a circular trajectory because the net forces acting on it are centripetal, so we write the equation of the centripetal force:

`F_(cp)=(mv^2)/(r)`

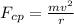
Since only the gravitational force is acting on the satellite this force is the net force, and thus, equal to the centripetal force:

`F_G=F_(cp)`

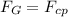
Which means:

`(GMm)/(r^2)=(mv^2)/(r)`

Or:

`(GM)/(r)=v^2`

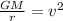
The velocity of the satellite is
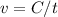`v=C/t`, where C is the circumference of the orbit, whose radius is obviously r:
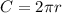`C=2\pi r`, so we can write:

`(GM)/(r)=((2\pi r)/(t))^2=(4\pi^2 r^2)/(t^2)`

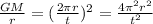
Which means:

`r^3=(GMt^2)/(4\pi^2)`

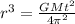
Which is Kepler's 3rd Law for a circular motion. We can write this as:

`r=\sqrt[3]{(GMt^2)/(4\pi^2)}`

Since there are 60 seconds in a minute and 60 minutes in an hour, using 24 hours we have:

`r=\sqrt[3]{((6.67*10^(-11)m^3/Kgs^2)(5.97*10^(24))(24*60*60s)^2)/(4\pi^2)}=42226910m=42227Km`

We could use the exact time of (23)(60)(60)+(56)(60)+(4.1) seconds, and in that case we would obtain r=42150Km