Answer:
f(x) will not have any roots.
Solution:
The roots of f(x) means the solution of f(x) = 0 which are the points where the function f(x) crosses the x axis. As the given equation, the highest power is 3, hence the equation will have total 3 roots.
Let us assume the three roots are a, b, c
Hence,
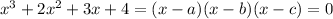
Multiplying the brackets we get
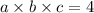
So a, b, c must be the factors of 4
The possibilities of factors of 4 are +1, -1, +2, -2, +4, -4
Substituting the values we get,
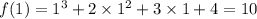
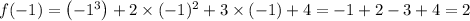
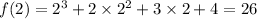
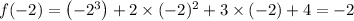
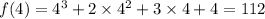
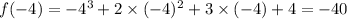
So, there are no values that satisfy the equation.
Hence f(x) will not have any roots.