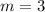Answer:
Explanation:
we know that
If two lines are perpendicular, then their slopes are opposite reciprocal (the product of their slopes is equal to -1)
step 1
Find the slope of the given line
we have
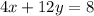
isolate the variable y
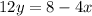
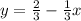
the slope of the given line is
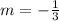
step 2
Find the slope
 of the perpendicular line to the given line
of the perpendicular line to the given line
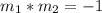
 ---> slope of the given line
---> slope of the given line
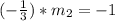
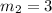
therefore
The value of m is