Question

Organisms are present in ballast water discharged from a ship according to a Poisson process with a concentration of 10 organisms/m3 (the article "Counting at Low Concentrations: The Statistical Challenges of Verifying Ballast Water Discharge Standards"† considers using the Poisson process for this purpose). What is the probability that one cubic meter of discharge contains at least 6 organisms?

Answer 1

There is a 93.28% probability that one cubic meter of discharge contains at least 6 organisms.

Explanation:

The number of organisms in a cubic meter of discharge is a Poisson process. So, we use the following definition:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

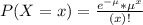
In which

x is the number of sucesses

`e = 2.71828` is the Euler number

`\mu` is the mean in the given time interval.

Organisms are present in ballast water discharged from a ship according to a Poisson process with a concentration of 10 organisms/m3. This means that
`\mu = 10`

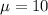
What is the probability that one cubic meter of discharge contains at least 6 organisms?

This is
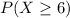`P(X \geq 6)`. We know that either we have less than 6 organisms, or we have at least 6 organism. The sum of the probabilities is decimal 1. So

`P(X < 6) + P(X \geq 6) = 1`

`P(X \geq 6) = 1 - P(X < 6)`

In which

`P(X < 6) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)`.

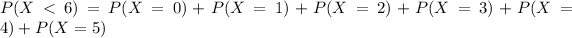Each one of these probabilities can be found by the poisson formula.

So

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-10)*10^(0))/((0)!) = 0.00004`

`P(X = 1) = (e^(-10)*10^(1))/((1)!) = 0.0004`

`P(X = 2) = (e^(-10)*10^(2))/((2)!) = 0.0023`

`P(X = 3) = (e^(-10)*10^(3))/((3)!) = 0.0078`

`P(X = 4) = (e^(-10)*10^(0))/((0)!) = 0.0189`

`P(X = 5) = (e^(-10)*10^(1))/((1)!) = 0.0378`

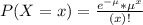
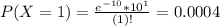
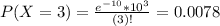
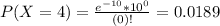
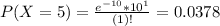
So

`P(X < 6) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)`

`P(X < 6) = 0.00004 + 0.0004 + 0.0023 + 0.0078 + 0.0189 + 0.0378 = 0.06724`

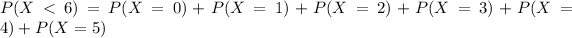
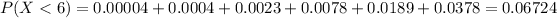
Finally

`P(X \geq 6) = 1 - P(X < 6) = 1 - 0.06724 = 0.9328`

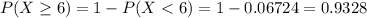
There is a 93.28% probability that one cubic meter of discharge contains at least 6 organisms.