Question

For the function f(x) = (x - 2)2 + 4, identify the vertex, domain, and range.

The vertex is (-2, 4), the domain is all real numbers, and the range is y? 4.
The vertex is (-2, 4), the domain is all real numbers, and the range is y s 4.
The vertex is (2, 4), the domain is all real numbers, and the range is y s 4.
The vertex is (2, 4), the domain is all real numbers, and the range is y 2 4.

Answer 1

The vertex is (2, 4), the domain is all real numbers, and the range is y≥ 4

Explanation:

we have

`f(x)=(x-2)^(2)+4`

This is the equation of a vertical parabola in vertex form

`f(x)=a(x-h)^(2)+k`

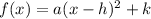
where

a is a coefficient

(h,k) is the vertex

if a > 0 the parabola open upward and the vertex is a minimum

if a < 0 the parabola open downward and the vertex is a maximum

In this problem we have

a=1

so

the parabola open upward and the vertex is a minimum

The vertex is the point (2,4)

The domain is the interval -----> (-∞,∞)

The domain is all real numbers

The range is the interval ----> [4,∞)

`y\geq 4`

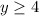
The range is all real numbers greater than or equal to 4