Answer:
Step-by-step explanation:
We need a value that multiplied by different integers gives us the values of the charges given. For this we grab the smallest charge, divide it by other integers (since the elemental charge should comply with this condition) and multiply it by the ones mentioned at the beginning to try to obtain the other charges. We should expect results that were never measured also (which "could be"). For now lets ignore all the
 and the units.
and the units.
We start then with 1.84. Maybe this is the elemental charge, and we would only need to multiply by other integers to obtain the rest of the charges. Lets see:
2(1.84)=3.68, we can't get 3.22, we will try with the next possibility,
2(1.84/2)=1.84, obviously,
3(1.84/2)=2.76, could be,
4(1.84/2)=3.68, again we can't get 3.22, we will try with the next possibility,
2(1.84/3)=1.23, could be,
3(1.84/3)=1.23, obviously,
4(1.84/3)=2.45, could be,
5(1.84/3)=3.07, could be,
6(1.84/3)=3.68, again we can't get 3.22, we will try with the next possibility,
2(1.84/4)=0.92, could be,
3(1.84/4)=1.38, could be,
4(1.84/4)=1.84, obviously,
5(1.84/4)=2.3, could be,
6(1.84/4)=2.76, could be,
7(1.84/4)=3.22, we obtained another value! Two to go,
8(1.84/4)=3.68, could be,
9(1.84/4)=4.14, we obtained another value! One to go,
10(1.84/4)=4.6, could be,
11(1.84/4)=5.06, could be,
11(1.84/4)=5.2, done!
Since (1.84/4)=0.46, the elemental charge (charge of the electron) could be
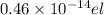 (since any value obtained by dividing this over any integer could be also the elemental charge, this problem is not determined).
(since any value obtained by dividing this over any integer could be also the elemental charge, this problem is not determined).