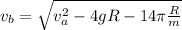Question

A block of mass 0.510 kg is pushed against a horizontal spring of negligible mass until the spring is compressed a distance x. The force constant of the spring is 450 N/m. When it is released, the block travels along a frictionless, horizontal surface to point circled A, the bottom of a vertical circular track of radius R = 1.00 m, and continues to move up the track. The speed of the block at the bottom of the track is vA = 13.7 m/s, and the block experiences an average frictional force of 7.00 N while sliding up the track. What is x? and what is the speed of the block if it reaches the top?

Answer 1

x=0.46m, speed=7.9m/s

Step-by-step explanation:

Using the concept of conservation of energy:

1. kinetic energy of mass m and velocity v:
`E_k=(1)/(2)mv^2`

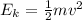
2. gravitational potential energy of mass m, grav. acc. g and height h:
`E_g=mgh`

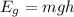
3. potential energy in a spring with spring constant k and displacement from equilibrium x:
`E_s=(1)/(2)kx^2`

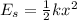
Calculating x:

`(1)/(2)mv_a^2=(1)/(2)kx^2`

`x=\sqrt{(m)/(k)}v_a`

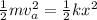
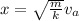
Calculating the speed:

`(1)/(2)mv_a^2 +mgh_a=(1)/(2)mv_b^2+mgh_b + W_(friction)`

`h_a=0, h_b=2R,W_(friction)=F_(friction)* distance=7\pi R`

`(1)/(2)mv_a^2=(1)/(2)mv_b^2+2mgR+7\pi R`

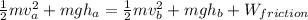
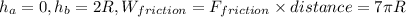
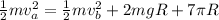
Solving for
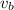`v_b`:

`v_b=\sqrt{v_a^2-4gR-14\pi(R)/(m)}`