Answer:]
At least 75% of the eruptions lasted between 1.24 and 5.6 minutes.
Explanation:
We are given the following information in the question:
n = 32
Mean = 3.42
According to Chebyshev's rule:
At least
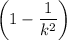 , percent of data lies within
, percent of data lies within
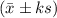 , where s is the standadrd deviation of the data and
, where s is the standadrd deviation of the data and
 is the mean of data.
is the mean of data.
For k = 2, we have
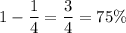
75% of data lies within the range of
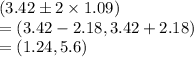
Thus, at least 75% of the eruptions lasted between 1.24 and 5.6 minutes.