Answer:
The energy is
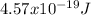 and the wavelength is
and the wavelength is
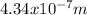 for the line in the spectrum of hydrogen that represents the movement of an electron from Bohr orbit with n = 2 to the orbit with n = 5.
for the line in the spectrum of hydrogen that represents the movement of an electron from Bohr orbit with n = 2 to the orbit with n = 5.
In what part of the electromagnetic spectrum do we find this radiation?
In the Ultraviolet part of the electromagnetic spectrum.
Step-by-step explanation:
The energy of the absorbed photon can be known by the difference in energy between the two states in which the transition is happening (In this case from n = 2 to n = 5):
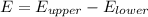 (1)
(1)
The permitted energy for the atom of hydrogen, according with the Bohr's model, is defined as:
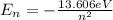 (2)
(2)
Or it can be expressed in Joules, since
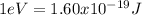
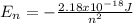 (3)
(3)
Where the value
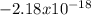 represents the energy of the ground state¹ and n is the principal quantum number.
represents the energy of the ground state¹ and n is the principal quantum number.
For the case of n = 2:
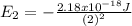
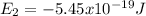
For the case of n = 5:
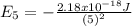
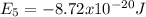
Replacing those values in equation (1) it is gotten:
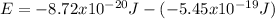
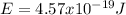
The wavelength can be determined by means of the Rydberg formula:
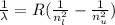 (4)
(4)
Where R is the Rydberg constant, with a value of
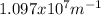
For this particular case
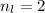 and
and
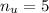 :
:
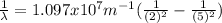
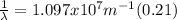
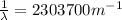
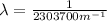
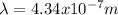
So the energy is
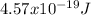 and the wavelength is
and the wavelength is
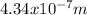 for the line in the spectrum of hydrogen that represents the movement of an electron from Bohr orbit with n = 2 to the orbit with n = 5.
for the line in the spectrum of hydrogen that represents the movement of an electron from Bohr orbit with n = 2 to the orbit with n = 5.
In what part of the electromagnetic spectrum do we find this radiation?
In the Ultraviolet part of the electromagnetic spectrum.
Key terms:
¹Ground state: State of minimum energy.