Question

You are given that a wheel has a radius of 2 feet and a spin rate of 10 revolutions per minute. Describe how you would determine the linear velocity, in feet per minute, of a point on the edge of the wheel.

Answer 1

Linear velocity of point on the edge of wheel having radius of 2 feet and spin rate of 10 revolution per minute is 125.71 feet per minute.

Solution:

Given that radius of wheel = 2 feet

There is a point on edge of the wheel .we need to determine linear velocity of that point.

Let’s first calculate distance covered by a point when 1 revolution of wheel is complete.

When one revolution is complete the distance traveled by a point on edge of the wheel will be equal to circumference of the wheel

`=2 \pi \mathrm{r}=2 \mathrm{x}\left((22)/(7)\right) * 2=(88)/(7) \mathrm{feet}`

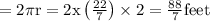
In one revolution, point covers distance of
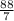`(88)/(7)` feet

So in 10 revolution, point covers distance of
`(88)/(7) * 10 = (880)/(7)`

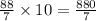
Given that in a minute, wheel takes 10 revolution.

Which means in a minute , point covers
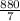`(880)/(7)` feet that is
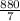`(880)/(7)` feet per minute = 125.71 feet per minute

Hence linear velocity of point on the edge of wheel having radius of 2 feet and spin rate of 10 revolution per minute is 125.71 feet per minute.