a. The average force exerted on the ball during the pitch is equal to 84.68N
b. Since the mass is increased, the force required for the pitcher has to increase too.
Why?
For the first part of the question (a), we need to convert all the units to work with the same system unit.
Converting the speed we have:
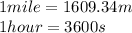

Now, calculating the force, we have:
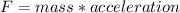
To calculate the acceleration we can use the following formula:

Therefore, calculating the force, we have:
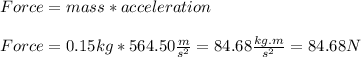
Hence, we have that the force exerted on the ball during the pich is equal to 84.68 N.
For the second part (b),
We need to assume that the final speed is maintaIned, so, since the equation to calculate the exerted force is a relationship between mass and acceleration (F=ma), if the mass of the object is increased, the force required need to be increased.
Have a nice day!