Answer:
Time taken the second tap to fill the pool alone = 15 hours.
Explanation:
Let the volume of pool be V.
The first tap can fill the pool in 10 hours.
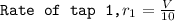
When the second tap was opened, the empty pool was filled in 6 hours. Here both taps are open
That is
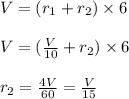
We need to find how long will it take the second tap to fill the pool alone.
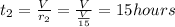
Time taken the second tap to fill the pool alone = 15 hours.