Answer:
0.36
Explanation:
We are given that Alison has all her money invested in two mutual funds A and B.
Probability that A will rise=
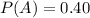
Probability that B rises given that A rise =
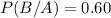
Probability that B will rise
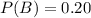
We have to find the probability that atleast one of the funds will rise in price.
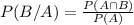
Substitute the values then we get
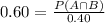
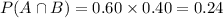
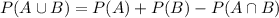
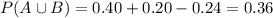
Hence, the probability that atleast one of the funds will rise in price=0.36