Question

What is the vertex of the function x2 - 6x + 8 = 0?

Answer 1

The vertex of the function
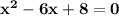`\bold{x^(2) -6 x + 8 = 0}`is (h,k) = (3 , -1)

Solution:

The vertex form of quadratic equation is generally given as,

`f(x) = a(x - h)^(2) + k`

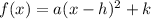
Where h,k is the vertex of the parabola.

From question, given that
`x^(2)-6 x+8=0` .

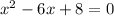we have to find the vertex of the function.

Let us first convert the given quadratic equation to vertex form (eqn 1)

`x^(2)-6 x+8=0`

`x^(2)-6 x=-8`

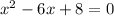
By adding “9” on both sides of equation, we get

`x^(2)-6 x+9=-8+9`

`x^(2)-6 x+9=1`

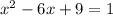
By using the identity
`(a-b)^(2)=a^(2)-2 a b+b^(2)` ,the right hand side of above equation becomes,

`(x-3)^(2)=1`

`(x-3)^(2)-1=0`

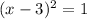
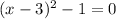
Now,the equation
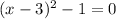`(x-3)^(2)-1=0` is of the vertex form.

By comparing
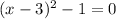`(x-3)^(2)-1=0` with
`a(x-h)^(2)+k`

we get the values of (h,k)

a = 1; h = 3; k = -1

hence the vertex of the function
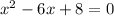`x^(2)-6 x+8=0` is (h,k) = (3 , -1)