Answer:
W=76.55 miles.metric tons
Step-by-step explanation:
Given that
Weight on the earth = 12 tons
So weight on the moon =12/6 = 2 tons
( because at moon g will become g/6)
As we know that
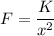
Here x= 1100 miles
F 2 tons
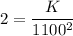
So
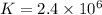
We know that
Work = F. dx
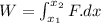
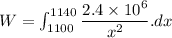
![W=-2.4* 10^6\left[(1)/(x)\right]_(1100)^(1140)](https://img.qammunity.org/2020/formulas/physics/high-school/2xkuh03ba9obcxhd5ol86igibyyxgw26oc.png)
![W=-2.4* 10^6\left[(1)/(1140)-(1)/(1100)\right]](https://img.qammunity.org/2020/formulas/physics/high-school/v8bgu4317i262dza2yadpjzoaduj6a7mct.png)
W=76.55 miles.metric tons