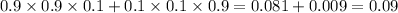Question

Everyone buying a pizza at JR's pizzeria gets a card that conceals either a J or an R. When the waxcovering is rubbed off, the chance is 90% that a J will appear. Different cards can be treated as havingindependent letters.Once a person has both a J and R, she is entitled to a free pizza. Note that, because the same letter cancome up on several successive purchases, that rule is not equivalent to one free pizza per two paid ones.If Pamela starts patronizing the pizzeria, find the probability that:a) She receives an R on her first purchase.b) Her first two purchases yield a J and R, in that order.c) She is eligible for a free pizza after her first two purchases.d) It takes her exactly three purchases to earn a free pizza.

Answer 1

The probability that She receives an R on her first purchase is 0.1

The probability that her first two purchases yield a J and R, in that order is 0.09

The probability that She is eligible for a free pizza after her first two purchases 0.18

The probability that It takes her exactly three purchases to earn a free pizza 0.09

Explanation:

Consider the provided information.

When the waxcovering is rubbed off, the chance is 90% that a J will appear.

Thus, the the chance or R will appear is 10%.

Part (a) She receives an R on her first purchase.

The probability of an R on first purchase is = 10/100 = 0.1

Part (b) Her first two purchases yield a J and R, in that order.

As we know the chance is 90% that a J will appear and 10% chance that R will appear.

Thus, the required probability is:

`(90)/(100) * (10)/(100)=0.9* 0.1=0.09`

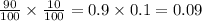
Part (C) She is eligible for a free pizza after her first two purchases.

There are two possible case:

Case I: First time J comes and second time R comes

Case II: First time R comes and second time J comes

Thus, the required probability is:

`0.9* 0.1+0.1* 0.9=0.09+0.09=0.18`

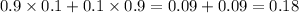
Part (d) It takes her exactly three purchases to earn a free pizza.

There are two possible case:

Case I: First time J comes, second times J comes and third time R comes

Case II: First time R comes, second times R comes and third time J comes

Thus, the required probability is:

`0.9* 0.9* 0.1+0.1* 0.1* 0.9=0.081+0.009=0.09`