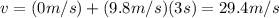Answer:
7)
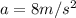
8)

9)
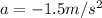
10)
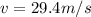
Step-by-step explanation:
For the problems 7, 8 and 9 we just apply the definition of acceleration, since no more information is given, which is:
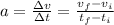
So for each problem we will have:
7)
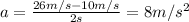
8)
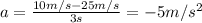
9)
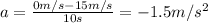
For the problem 10, we use the equation of velocity in accelerated motion:

Since the ball starts from rest and the acceleration is that of gravity (we take the downward direction positive), we have: