Question

A hawk is flying horizontally at 20.0 m/s in a straight line, 140 m above the ground. A mouse it has been carrying struggles free from its talons. The hawk continues on its path at the same speed for 2.00 s before attempting to retrieve its prey. To accomplish the retrieval, it dives in a straight line at constant speed and recaptures the mouse 4.00 m above the ground.

a.) Assuming no air resistance acts on the mouse, find the diving speed of the hawk.
b.) What angle did the hawk make with the horizontal during its descent?
c.) For what time interval did the mouse experience free fall?

Answer 1

a) V = 46.736m/s

b) θ = 64.66°

c) t ∈ [0, 5.22]s

Step-by-step explanation:

First we need the instant when the hawk catches the mouse.

For the mouse:

`X_M = V_H*t = 20*t`

`Y_M = Y_(oM) - (g*t^2)/(2)`
`4 = 140 - (10*t^2)/(2)`

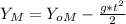
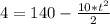
From the y-axis equation we get the time of flight of the mouse:

`t = \sqrt{(2*\Delta Y)/(g) }=5.22s`

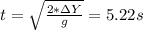
With this time we calculate the x-position of the mouse:

`X_M = 20*5.22 = 104.4m`

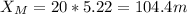
For the hawk:

`X_H = V_(oH)*to + V_(XDive)*(t-2)=20*2+V_(XDive)*(5.22-2)=X_M`

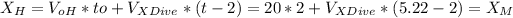
Solving for x-component of the dive velocity:

`V_(XDive) = 20m/s`

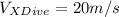
On the y-axis:

`Y_H = 140+V_(YDive)*(t-2)=140+V_(YDive)*(5.22-2)=4`

Solving for the y-component of the dive velocity:

`V_(YDive) = -42.24m/s`

Now, the speed will be given by (part a):

`V_(Dive)=\sqrt{V_(XDive)^2+V_(YDive)^2}=46.736m/s`

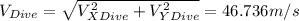
The angle of the dive will be (part b):

`\theta = atan((V_(YDive))/(V_(XDive)) )=64.66°`

For part c, the mouse experienced free fall from t=0 until it was catched at t=5.22s