Question

student conducts a high temperature experiment using a thermister with a guaranteed accuracy of +/- 1.3 degrees Fahrenheit. The student takes an initial set of 11 measurements,and calculates a sample average of 224 and a sample deviation of 19.8 degrees. Assuming a confidence level of 99%, estimate the total number of samples needed to ensure a total measurement uncertainty less than 3.5 degrees. (the number of samples should be an integer)

Answer 1

213 samples needed for 99% confidence interval

Explanation:

We know that:

minimum size of sample needed to be sure about total measurement less than 3.5 degree is given as

`n = [(z_(\alpha/2)*  s)/(E)]^2`

where,

s is standard deviation = 19.8 degree

E IS MARGIN OF ERROR = 3.5 degree

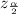`z _{(\alpha)/(2)}` right tail critical value of

Z
`z _{(\alpha)/(2)}  = z _{(0.01)/(2)} = z_(0.005) = 2.58`

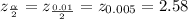
so, minimum size of sample needed is

`n = [(2.58* 19.8)/(3.5)]^2`

n = 213.02

Therefor 213 samples needed for 99% confidence interval