Solutions:
Part A:
Let

As we know that the values at the point of intersection are the values that satisfy both the equation at that particular point.
So at insertion point,
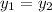
Hence
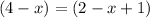
Part 2:
The problem asked to make tables to find the solution to
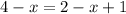
If we take the first equation,
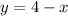
then, the table for (x,y) is
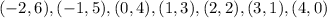
if we take the second equation,
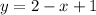
then the table for (x,y) is

Part 3:
We can solve the equation
 graphically by drawing the line
graphically by drawing the line
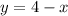 and
and
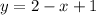 in the graph. The intersecting point of both the lines will be the solution.
in the graph. The intersecting point of both the lines will be the solution.