Question

An elementary school is offering 3 language classes: one in Spanish, one in French,and one in German. The classes are open to any of the 100 students in the school.There are 28 students in the Spanish class, 26 in the French class, and 16 in theGerman class. There are 12 students that are in both Spanish and French, 4 thatare in both Spanish and German, and 6 that are in both French and German. Inaddition, there are 2 students taking all 3 classes.

(a) If a student is chosen randomly, what is the probability that he or she is not in any of the language classes?(b) If a student is chosen randomly, what is the probability that he or she is taking exactly one language class?(c) If 2 students are chosen randomly, what is the probability that at least 1 is taking a language class?

Answer 1

A. 0.5

B. 0.32

C. 0.75

Explanation:

There are

• 28 students in the Spanish class,
• 26 in the French class,
• 16 in the German class,
• 12 students that are in both Spanish and French,
• 4 that are in both Spanish and German,
• 6 that are in both French and German,
• 2 students taking all 3 classes.

So,

• 2 students taking all 3 classes,
• 6 - 2 = 4 students are in French and German, bu are not in Spanish,
• 4 - 2 = 2 students are in Spanish and German, but are not in French,
• 12 - 2 = 10 students are in Spanish and French but are not in German,
• 16 - 2 - 4 - 2 = 8 students are only in German,
• 26 - 2 - 4 - 10 = 10 students are only in French,
• 28 - 2 - 2 - 10 = 14 students are only in Spanish.

In total, there are

2 + 4 + 2 + 10 + 8 + 10 +14 = 50 students.

The classes are open to any of the 100 students in the school, so

100 - 50 = 50 students are not in any of the languages classes.

A. If a student is chosen randomly, the probability that he or she is not in any of the language classes is

`(50)/(100) =0.5`

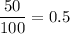
B. If a student is chosen randomly, the probability that he or she is taking exactly one language class is

`(8+10+14)/(100)=0.32`

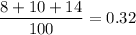
C. If 2 students are chosen randomly, the probability that both are not taking any language classes is

`0.5\cdot 0.5=0.25`

So, the probability that at least 1 is taking a language class is

`1-0.25=0.75`