Question

n a sample of seven​ cars, each car was tested for​ nitrogen-oxide emissions​ (in grams per​ mile) and the following results were​ obtained: 0.12​, 0.08​, 0.18​, 0.07​, 0.12​, 0.14​, 0.15 . Assuming that this sample is representative of the cars in​ use, construct a 98​% confidence interval estimate of the mean amount of​ nitrogen-oxide emissions for all cars. If the EPA requires that​ nitrogen-oxide emissions be less than 0.165 g divided by mi​, can we safely conclude that this requirement is being​ met?

Answer 1

(0.0772,0.1688)

Explanation:

We are given the following data set:

0.12​, 0.08​, 0.18​, 0.07​, 0.12​, 0.14​, 0.15

n = 7

a) Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(0.86)/(7) = 0.123`

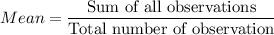
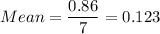
Sum of squares of differences = 0.000008163265305 + 0.001836734694 + 0.003265306122 + 0.002793877551 + 0.000008163265305 + 0.0002938775509 + 0.0007367346937 = 0.008942857142

`S.D = \sqrt{(0.008942857142)/(6)} = 0.0386`

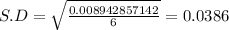
Confidence interval:

`\mu \pm t_(critical)(\sigma)/(√(n))`

Putting the values, we get,

`t_(critical)\text{ at}~\alpha_(0.02)\text{ and degree of freedom 6} = \pm 3.142`

`0.123 \pm 3.142((0.0386)/(√(7)) ) = 0.123 \pm 0.0458 = (0.0772,0.1688)`

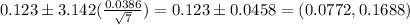
b) No, this requirement is not met because the interval contains value greater than 0.165 g as well.