Question

Write the point-slope form of the line that passes through (-8,2) and is perpendicular to a line with a slope of -8 include all of your work in your final answer.

Answer 1

The point-slope form of the line that passes through (-8,2) and is perpendicular to a line with a slope of -8 is x -8y +24 = 0

Solution:

The point slope form of the line that passes through the points
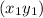`\left(x_(1) y_(1)\right)` and perpendicular to the line with a slope of “m” is given as

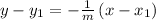`y-y_(1) = -(1)/(m)\left(x-x_(1)\right)` ---- eqn 1

Where “m” is the slope of the line.
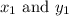`x_(1) \text { and } y_(1)` are the points that passes through the line.

From question, given that slope “m” = -8

Given that the line passes through the points (-8,2).Hence we get

`x_(1 ) = -8 ; y_(1) = 2`

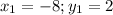
By substituting the values in eqn 1 , we get the point slope form of the line which is perpendicular to the line having slope -8 can be found out.

`y - 2 = (1)/(8)(x + 8)`

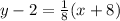
On cross multiplying we get,

8y - 16 = (x+8)

8y – 16 = x +8

On rearranging we get,

x -8y +16 + 8 = 0

x -8y +24 = 0

hence the point slope form of given line is x -8y +24 = 0