Answer:
The probability of obtaining a sample mean below 19.91 fl oz. is 0.0041
Explanation:
Consider the provided information.
The amount of soft drink poured into each bottle follows a normal distribution with mean 20 fl oz and standard deviation 0.17 fl oz.
A Sample of 25 bottles were randomly selected and the amount of soft drink in each bottle was measured.
The mean amount of soft drink in each bottle was calculated to be 19.91 fl oz.
Thus we have mean 20 fl oz
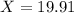 σ=0.17 and n=25.
σ=0.17 and n=25.
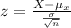
Substitute the respective values.
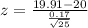
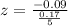
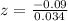
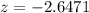
According to normal distribution table:
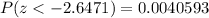
The probability of obtaining a sample mean below 19.91 fl oz. is 0.0041