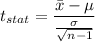Question

A candy factory that produces chocolate bars claims each bar weighs 50 grams, at least that is what is printed on the label. Of course, there is bound to be a little variation. An inspector randomly chooses 9 bars from one day's output of 4000 bars. The average weight of the 9 bars is only 47 grams. The inspector wishes to test the null hypothesis that the factory is doing what it is supposed to on this day against the alternative that the company is cheating the consumer. Assume that the weights of all the candy bars that are produced follow the normal curve with a SD of 3 grams. a. Which significance test should be used?

Answer 1

We use T-test to perform this hypothesis.

Explanation:

We are given the following in the question:

Population mean, μ = 50 grams

Population standard deviation, σ = 3 grams

Sample mean,
`\bar{x}` = 47 grams

Sample size, n = 9

First, we design the null and the alternate hypothesis

`H_(0): \mu = 50\text{ grams}\\H_A: \mu < 50\text{ grams}`

We use T-test to perform this hypothesis. because the sample size is 9 which is less than 30, hence it does not follows a normal distribution.

Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n-1)) }`