Answer:
a) 0.00673
b)0.9596
Explanation:
Let be X the random variable : ''Number of deaths from this disease''
X ~ P(λt)
Where λ is number of events per unit time and λt is number of events over time period t
In our exercise t = 1 year
λ : lambda
The probability function for X is :
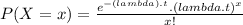
x ≥ 0
a)
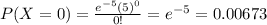
b)
![P(X\geq 2)=1-P(X<2)=1-[P(X=0)+P(X=1)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/611k0pkle8d6n00xys41i7mmgdqjh4aivz.png)
![P(X\geq 2)=1-[e^(-5)+(e^(-5).(5)^1)/(1!)}]=1-[e^(-5)+5(e^(-5))]=1-6(e^(-5))=0.9596](https://img.qammunity.org/2020/formulas/mathematics/high-school/judgyifmiw9d2a6phquzirv081q5zcsyi5.png)