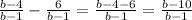Answer:
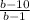
Explanation:
We start by factoring out all polynomials in the expression:
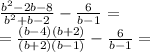
where we can simplify the factor (b+2) that appears in numerator and denominator of the first rational expression, to reduce it to:

Now we can combine both rational expressions since they share the same denominator: