Question

What are the coordinates of the endpoints of the midsegment for △ABC that is parallel to BC¯¯¯¯¯? Enter your answers in the boxes. ( , ) and ( , )

Answer 1

(4,2) and (8,2).

Answer 2

(4,2) and (8,2)

Explanation:

Using the image attached, you can observe that the midsegment parallel to BC has to be placed from the AB midpoint to the AC midpoint.

To find a midpoint we need to use the following formula:

`m_(AB)=((x_(1)+x_(2))/(2) ,(y_(1)+y_(2))/(2) )`

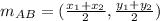
Where
`(x_(1),y_(1))` represents the coordinates of point A and
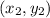`(x_(2),y_(2))` represents the coordinates of B.

From the image you can see that coordinates are
`(7,6)` and
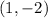`(1,-2)`, using the formula, we have

`m_(AB)=((7+1)/(2) ,(6+(-2))/(2) )\\m_(AB)=((8)/(2) ,(4)/(2) )\\m_(AB)=(4 ,2 )`

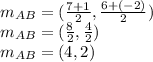
This means that the beginning of the midsegment is at
`m_(AB)=(4 ,2 )`

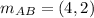
Now, we do the same process to find the end point of the midsegment. The points that we are gonna use this time are
`(7,6)` and
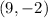`(9,-2)`. Using the formula we have

`m_(AC)=((x_(1)+x_(2))/(2) ,(y_(1)+y_(2))/(2) )\\m_(AC)=((7+9)/(2) ,(6+(-2))/(2) )\\m_(AC)=((16)/(2) ,(4)/(2) )\\m_(AC)=(8 ,2)`

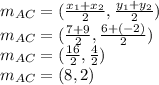
Therefore, the endpoints of the midsegment for △ABC that is parallel to BC are at (4,2) and (8,2)